|
|
|
Zadania sprawdzianu na lekcje matematyki |
|
|
|
 |
|
W roku szkolnym 2002/2003 w Kujonie małopolskiego dodatku Gazety Wyborczej prowadzony był cykl
związany z przygotowaniem
uczniów do sprawdzianu. Poniżej prezentujemy wybrane zadania z tego
cyklu wraz z komentarzami
egzaminatora sprawdzianu. |
|
|
|
Przykłady tekstów, zadań i komentarzy do zadań |
|
|
|
W zadaniach zamkniętych spośród czterech zaproponowanych odpowiedzi jedna
jest prawdziwa. Wystarczy nieraz przeczytać uważnie tekst, innym razem
trzeba dokonać analizy warunków zadania. |
|
|
|
 |
|
Zaczęło padać za piętnaście dziewiąta wieczorem i
padało do wpół do ósmej rano następnego dnia. Ile czasu padał deszcz?
| A. 11 godz. 45 min |
B. 10 godz. 15 min |
C. 10 godz. 45 min |
D. 11 godz. 15 min |
|
|
 |
|
Skoro
zaczęło padać za piętnaście dziewiąta wieczorem i padało do wpół do
ósmej rano to znaczy, że przed północą padało trzy godziny i
piętnaście minut, a po północy siedem i pół godziny, zatem łącznie
padało 10 godzin 45 minut, czyli prawidłową odpowiedzią jest
odpowiedź C. |
|
|
 |
|
Bociany przyleciały do swojego starego gniazda 5
kwietnia. Po 140 dniach znów odleciały do ciepłych krajów. Bociany
odleciały w
A. pierwszej połowie września.
B. pierwszej połowie sierpnia.
C. drugiej połowie września.
D. drugiej połowie sierpnia. |
 |
|
Miesiąc ma około 30 dni. 140 dni to około 4 miesiące
(120 dni)
i 20 dni, cztery miesiące od 5 kwietnia do 5 sierpnia, no i jeszcze
około 20 dni, a to już na pewno druga połowa sierpnia, czyli
odpowiedź D. Można inaczej: wrzesień następuje pięć miesięcy
(około 150 dni) po kwietniu. Odpowiedzi A i C odpadają, 140 dni to o
10 mniej od 150, czyli od „mniej więcej” 5 września trzeba się
cofnąć o 10 dni, a to właśnie druga połowa sierpnia.
|
|
|
 |
|
Malwina kupiła pod koniec maja pierwsze czereśnie.
Za 20 dekagramów zapłaciła 1,60 zł. W czerwcu czereśnie były już dwa
razy tańsze. Ile kosztował 1 kilogram czereśni w czerwcu?
|
A. 8 zł |
B. 0,8 zł |
C. 4 zł |
D. 0,4 zł |
|
 |
|
W czerwcu były czereśnie dwa razy tańsze niż w maju, zatem 20
dekagramów czereśni w czerwcu kosztowało dwa
razy mniej niż tyle samo w maju. Cena jednego kilograma czereśni w
czerwcu musiała być na pewno wyższa niż 20 dekagramów czereśni w
maju, zatem odpowiedzi B i D można od razu odrzucić. Gdyby 1 kg
czereśni w maju kosztował 8 zł
| to 20 dag |
|
. 8 zł czyli 1,60 zł, więc odpowiedź A jest błędna |
Pozostała do
wyboru odpowiedź C, rzeczywiście 4 zł to dwa razy mniej niż 8 zł. |
|
|
 |
|
| Jesienią świstak gromadzi pod skórą zapas tłuszczu na zimę,
powiększając aż o |
|
masę |
swego ciała. Na początku lata świstak ważył 3 kg. Ile
kilogramów będzie ważył tuż przed zapadnięciem w sen zimowy?
|
 |
|
Świstak powiększa masę ciała, odpada więc odpowiedź A (2 kg to mniej
niż 3 kg). Powiększa aż o ⅔ masy swego
ciała, czyli więcej niż o połowę. Na początku lata ważył 3 kg, czyli
przed zapadnięciem w sen zimowy waży więcej niż 4 ½ kg. Jedynie
odpowiedź B spełnia ten warunek. |
|
|
 |
|
Rok 2003 to:
A. pierwsza połowa XX wieku.
B. pierwsza połowa XXI wieku.
C. druga połowa XX wieku.
D. druga połowa XXI wieku. |
 |
|
Poprawna jest odpowiedź B. W latach 2001-2050 trwa pierwsza połowa
XXI wieku. |
|
|
 |
|
Najdłuższą trasą autobusową, jaką można znaleźć w rozkładach
jazdy jest trasa z Caracas w Wenezueli do Buenos Aires w Argentynie. Liczy
ona 9660 km. Podróż trwa 214 godzin wliczając 12 godzin postoju w Santiago w
Chile i 24 godziny postoju w stolicy Peru – Limie. |
|
Focus ekstra nr 1/2001- LATO 2001. |
|
|
|
|
|
|
|
 |
|
Czas jazdy autobusem tą trasą, z pominięciem postojów w
Santiago i Limie, wyrażony w godzinach, można opisać wyrażeniem
|
A. 214 +12 +24 |
B. 214 – 24 + 12 |
C. 214 - (24 + 12) |
D. 214 + (24 – 12) |
|
 |
|
Na podstawie przeczytanego tekstu wiadomo, że w całkowity
czas podróży został wliczony czas długotrwałych postojów w Limie i Santiago.
W związku z tym od 214 godzin trzeba odjąć łączny czas przeznaczony na oba
postoje, takiej sytuacji odpowiada jedynie wyrażenie z punktu C. |
|
|
|
|
|
|
|
 |
|
214 godzin to:
A. 9 dób i 2 godziny.
B. 8 dób i 10 godzin.
C. 8 dób i 22 godziny.
D. 17 dób i 10 godzin.
|
 |
|
Doba ma 24 godziny, 10 dób to 240 godzin, więc na pewno
odpowiedź D jest błędna. 9 dób to 216 godzin, czyli odpada również odpowiedź
A. 214 godzin to o dwie godziny mniej niż 9 dób, a więc warunek ten spełnia
odpowiedź C. |
|
|
|
|
|
|
|
 |
|
Autobus wyruszył w podróż tą trasą w poniedziałek o godzinie
8:00 rano. Jadąc zgodnie z rozkładem jazdy przyjedzie na miejsce o godzinie
szóstej rano w:
A. następny wtorek.
B. następną środę.
C. następny poniedziałek.
D. następną niedzielę.
|
 |
|
Do następnego poniedziałku mija 7 dób, czyli 9 dób (216
godzin) mija we środę o godzinie 8:00, a 214 godzin także we środę tylko
o godzinie 6:00. Poprawna jest odpowiedź B. |
|
|
|
|
|
|
|
 |
|
Autobus zakończył podróż tą trasą, zgodnie z rozkładem
jazdy, w samo południe 1 czerwca. Podróż ta rozpoczęła się
A. 22 maja o godzinie 14:00.
B. 23 maja o godzinie 12:00.
C. 22 maja o godzinie 12:00.
D. 23 maja o godzinie 14:00.
|
 |
|
Podróż trwała 214 godzin, czyli dwie godziny mniej niż 9
dób. Maj ma 31 dni. Od godziny dwunastej 22 maja do południa 1 czerwca mija
dziesięć dób, czyli 9 mija w południe 23 maja. Zatem podróż musiała
rozpocząć się 23 maja o godzinie 14:00. |
|
|
|
|
|
|
|
 |
|
Średnia szybkość autobusu uzyskana podczas jazdy na tej
trasie (z pominięciem czasu dwóch długich postojów w Limie i Santiago)
wynosi
A. ponad 60 km/ godzinę.
B. około 54 km/ godzinę.
C. około 45 km/ godzinę.
D. około 20 km/godzinę.
|
 |
|
Średnią szybkość liczymy jako stosunek długości trasy (9660
km) do czasu przejazdu autobusem (178 godzin) tej drogi. Na pewno szybkość
ta będzie większa od 48 km/godzinę, bo 9660 : 178 > 9660 : 200 > 48, ale mniejsza od 60 km/godzinę,
bo 9660 : 60 < 161 < 178. Można sprawdzić, że właściwą odpowiedzią jest odpowiedź B.
|
|
|
|
|
 |
|
W szkole podstawowej w klasach szóstych jest 92 uczniów, w
piątych dwa razy tyle, a w czwartych o 13 uczniów mniej niż w szóstych. |
|
|
|
|
|
|
|
 |
|
Ilu uczniów jest w klasach piątych?
|
 |
|
W klasach piątych jest dwa razy tyle uczniów, co w klasach
szóstych, czyli na pewno więcej niż 92. Spośród podanych odpowiedzi jedynie
liczba 184 jest większa od liczby 92. Rzeczywiście 184 to dwa razy więcej
niż 92. Zatem prawidłową odpowiedzią jest odpowiedź B. |
|
|
|
|
|
|
|
 |
|
Ilu uczniów jest w klasach czwartych?
|
A. 81 |
B. 105 |
C. 79 |
D. 115 |
|
 |
|
Z tekstu zadania wynika, że w klasach czwartych jest mniej
uczniów niż w klasach szóstych, czyli mniej, niż 92, więc trzeba odrzucić
odpowiedzi B i D. Należy sprawdzić, która z pozostałych liczb spełnia
warunki zadania. Oczywiście liczba 79 jest o 13 mniejsza od 92. Poprawna
jest odpowiedź C. |
|
|
|
|
|
 |
|
Janek rozpoczął w szkole lekcje o godzinie 8:55, zakończył o
godzinie 12:25. Jak długo trwały zajęcia w szkole?
|
A. 4 godz. 20 minut |
B. 4 godz. 30 minut |
C. 3 godz. 20 minut |
D. 3 godz. 30 minut |
|
 |
|
Między godziną 8:55, a 12:25 upływa tyle samo czasu, co
miedzy godziną 9:00 a 12:30, czyli 3 i pół godziny. Należy wybrać odpowiedź
D. |
|
|
|
|
|
 |
|
Przerwa świąteczna w nauce rozpoczęła się 21 grudnia i
trwała do Nowego Roku. Ile dni trwała przerwa świąteczna?
|
 |
|
Do rozpoczęcia przerwy świątecznej upłynęło 20 dni grudnia.
Grudzień ma 31 dni. Zatem przerwa świąteczna trwała przez 11 dni grudnia i
jeden dzień stycznia (Nowy Rok). Prawidłowa jest odpowiedź C. |
|
|
|
 |
|
Na naukę w domu Janek poświęcił 1 i 3/4 godziny, a na
czytanie książki 3/4 godziny. |
|
|
|
|
|
|
|
 |
|
Ile godzin łącznie Janek poświecił na naukę i czytanie
książki?
|
A. 2 i 1/2 |
B. 2 i 1/4 |
C. 2 i 3/4 |
D. 2 i 3/8 |
|
 |
|
Aby obliczyć czas poświęcony na naukę i czytanie książki
należy dodać do siebie podane wielkości: 1 ¾ + ¾ = 2 ½. Właściwą odpowiedzią
jest odpowiedź A. |
|
|
|
|
|
|
|
 |
|
Ile minut Janek poświęcił na naukę?
|
A. 175 |
B. 135 |
C. 75 |
D. 105 |
|
 |
|
Najważniejsze to pamiętać, że 1
godzina ma 60 minut.1¾ godziny to więcej niż półtorej godziny (90
minut), a mniej niż dwie godziny
(120 minut). Warunki zadania spełnia odpowiedź D. |
|
|
|
|
|
|
|
 |
|
Ile minut Janek poświecił na czytanie książki?
|
 |
|
¾ godziny to więcej niż pół godziny (30 minut), a mniej niż
godzina (60 minut). Warunki zadania spełnia odpowiedź B. |
|
|
|
|
|
W arkuszu sprawdzianu – oprócz zadań zamkniętych wielokrotnego wyboru,
w których trzeba wybrać prawidłową odpowiedź spośród zaproponowanych – są
zadania otwarte. Te zadania należy wykonywać w przeznaczonym na to miejscu.
Rozwiązanie powinno być tak przedstawione, aby egzaminator mógł odczytać tok
rozumowania ucznia. Jeśli w zadaniu nie ma wskazanej żadnej metody, którą należy
zastosować, wybór sposobu dochodzenia do wyniku należy do ucznia. Są zadania,
które można rozwiązać kilkoma metodami. Poniżej prezentujemy przykład takiego zadania.
|
|
|
 |
|
Suma dwóch liczb równa się 60, a iloraz większej przez
mniejszą wynosi 3. Jakie to liczby? |
 |
|
I sposób rozwiązania zadania – za pomocą równania: Budując równanie należy przyjąć sobie jedną z szukanych
wielkości za niewiadomą. W tym zadaniu oznaczamy przez x mniejszą z liczb.
Z informacji, że iloraz tych liczb wynosi 3, wynika, że jedna z nich jest
trzy razy większa od drugiej. Zatem druga z liczb jest równa 3x. Drugi
warunek zadania mówi, że sumą tych liczb jest 60, czyli: x + 3x = 60
4x = 60 x = 15 3x = 45 Po rozwiązaniu równania należy sprawdzić, czy otrzymane
liczby spełniają warunki zadania i sformułować odpowiedź.
|
|
 |
|
II sposób rozwiązania zadania – za pomocą rysunku:
Można przyjąć, że szukane liczby ilustrują długości dwóch
odcinków, z których jeden jest trzy razy dłuższy od drugiego, a razem mają
długość równą 60 jednostek.
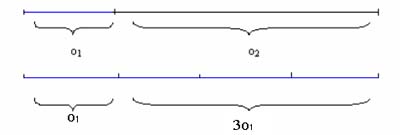
Porównując długości odcinków na rysunku, można obliczyć
wartości obu liczb. Po obliczeniu należy sprawdzić, czy otrzymane liczby
spełniają warunki zadania i sformułować odpowiedź.
|
|
 |
|
III sposób rozwiązania zadania – za pomocą rachunków na liczbach:
W zadaniu szukamy dwóch liczb, z których jedna jest
trzykrotnością drugiej. Zatem suma pierwszej z szukanych liczb i jej
trzykrotności daje liczbę cztery razy większą od pierwszej liczby. Wystarczy
podzielić 60 przez 4, aby obliczyć pierwszą liczbę, a otrzymaną wartość
pomnożyć przez 3. W ten sposób wyliczymy drugą z liczb.
Liczba pierwsza: 60 : 4 = 15
Liczba druga: 15 ´ 3 = 45
Po obliczeniu należy sprawdzić, czy otrzymane liczby
spełniają warunki zadania i sformułować odpowiedź. |
|
|
|
|
Oto przykłady innych zadań tego typu. Czym rozwiązania tych
zadań będą się różnić, a w czym będą podobne? W poniższych przykładach
pozostawiono miejsce na komentarz puste. Proponujemy nauczycielom podjęcie próby
napisania rad dla uczniów. |
|
|
|
 |
|
Dwa odcinki mają razem 60 cm długości. Jeden jest trzy razy
krótszy od drugiego. Ile centymetrów długości ma każdy z tych odcinków? |
 |
|
|
|
|
|
|
 |
|
Ojciec i syn mają razem 60 lat. Ojciec jest trzy razy
starszy od syna. Ile lat ma każdy z nich? |
 |
|
|
|
|
|
|
 |
|
Kasia i Bartek mają razem 60 znaczków. Kasia ma trzy razy
mniej znaczków niż Bartek. Po ile znaczków ma każde z nich? |
 |
|
|
|
|
|
|
Każda z form zadań pisemnych ma zastosowanie w zadaniach
testowych
z matematyki. Jednak dobór poszczególnych form zadań w teście zależy od tego, co
chcemy badać. Na przykładzie kilku zadań służących do badania znajomości
definicji równoległoboku można porównać jak, w zależności od formy zadania,
badana jest ta umiejętność. |
|
|
|

typ
(PF) |
|
W wolne miejsce wpisz literę P, jeśli zdanie jest prawdziwe,
a literę F, jeśli zdanie jest fałszywe.
| |
A. |
Równoległobok to taki czworokąt, który ma co najmniej jedną
parę boków równoległych. |
|
|
|
| |
B. |
Równoległobok to taki czworokąt, który ma dokładnie jedną
parę boków równoległych. |
|
|
|
| |
C. |
Równoległobok to taki czworokąt, który ma dwie pary boków
równoległych. |
|
|
|
|
 |
|
W tym zadaniu uczeń wybiera poprawną definicję
równoległoboku. Może to zadanie wykonać porównując podane określenia z tym,
które zna. |
|
|
|
|

typ
(D) |
|
Przy nazwie figury wpisz literę R, jeśli jest ona
równoległobokiem, literę N, jeśli jest to nazwa figury nie będącej
równoległobokiem, natomiast O, jeśli nie można stwierdzić jednoznacznie tego
faktu.
| kwadrat |
|
| prostokąt |
|
| romb |
|
| trapez prostokątny |
|
| trapez równoramienny |
|
| deltoid |
|
| latawiec |
|
|
 |
|
W tym zadaniu uczeń musi przypomnieć sobie podstawowe
informacje o poszczególnych wielokątach i dokonać klasyfikacji zgodnie z
podanymi kryteriami. Rozwiązując zadanie musi odnosić się do definicji
poszczególnych czworokątów. |
|
|
|
|
 |
|
Pod rysunkiem figury wpisz literę R, jeśli jest ona
równoległobokiem, literę N, jeśli jest to figura nie będąca
równoległobokiem. |
|
typ
(D) |
|
 |
|
Uczeń obserwując przedstawione figury musi dokonać
klasyfikacji zgodnie z podanymi kryteriami. Do rozwiązania tego zadania nie
jest mu potrzebna znajomość definicji innych czworokątów niż równoległobok. |
|
|
|
|

typ
(L) |
|
| Uzupełnij brakujące określenie. |
| 1. |
________________ to taki czworokąt, który ma dwie pary boków
równoległych.
|
|
2. |
Równoległobok to taki wielokąt, który
_________________________________. |
|
 |
|
W zadaniu 1 z luką uczeń musi uzupełnić brakujący wyraz. W
tym wypadku poszukuje nazwy czworokąta spełniającego podany warunek. W
zadaniu 2 z luką uczeń powinien dopisać, jakie warunki musi spełniać
wielokąt, aby był równoległobokiem. Zadanie 1 jest łatwiejsze niż zadanie 2.
Każde z tych zadań można zamienić na zadania krótkiej odpowiedzi badające te
same umiejętności. |
|
|
|
|

typ
(KO) |
|
1. Jaki czworokąt nazywamy równoległobokiem?
2. Jaki wielokąt nazywamy równoległobokiem?
3. Jaką figurę nazywamy równoległobokiem?
|
 |
|
W każdym z tych zadań pytamy o równoległobok, ale punktem
wyjściowym definicji jest za każdym razem inna figura, co czyni te zadania
zadaniami o różnym stopniu trudności. |
|
|
|
|

typ
(RO) |
|
Narysuj cztery różne czworokąty, nie będące równoległobokami
i napisz, przy każdym z nich, dlaczego nie jest równoległobokiem. |
 |
|
W zadaniu tym uczeń wykonuje rysunki figur spełniających
podany warunek i uzasadnia swój wybór. |
|
|
|
|
Na tych przykładach widać, że, mimo iż każde z tych zadań bada
znajomość definicji równoległoboku, to uczeń prawie za każdym razem znalazł się
w innej sytuacji i zupełnie inaczej wykorzystywał znajomość definicji
równoległoboku. Należy sobie uświadomić, że stwierdzenie, iż każde z tych zadań
bada znajomość definicji równoległoboku jest zbyt ogólne i wymaga za każdym
razem doprecyzowania. Przydatność każdego z tych zadań jest inna, bo co innego
badać, czy uczeń potrafi poprawnie wypowiedzieć definicję, co innego, umieć ją
wykorzystać do klasyfikowania obiektów a jeszcze, co innego budować przykłady i
kontrprzykłady dla definiowanego pojęcia. Niejednokrotnie tworzy się zadania w
różnych formach do analogicznej sytuacji realistycznej. Np.:
|
|
|
|

typ
(RO) |
|
Kasia i Marysia mają razem 24 lata. Kasia jest dwa razy
starsza od Marysi. Ile lat temu Marysia była trzy razy młodsza od Kasi? |
 |
|
Uczniowie rozwiązując to zadanie zazwyczaj najpierw
obliczają wiek każdej
z dziewcząt, a potem wyznaczają szukaną wielkość. Zatem zadanie to jest
zadaniem wieloetapowym. Prześledzenie rozwiązania daje możliwość
zaobserwowania toku rozumowania ucznia i pozwala wnioskować o tym, jakie
metody rozwiązania uczniowie preferują. |
|
|
|
|

typ
(KO) |
|
Kasia i Marysia mają razem 24 lata. Kasia jest dwa razy
starsza od Marysi. Ile lat ma każda z nich? |
 |
|
To zadanie typu KO to część poprzedniego zadania RO. W
stosunku do poprzedniego zadania jest zadaniem łatwiejszym, mniej
czasochłonnym, a daje także możliwość zaobserwowania toku rozumowania ucznia
i pozwala wnioskować o tym, jakie metody rozwiązania uczniowie preferują. |
|
|
|
|

typ
(L) |
|
Kasia i Marysia mają razem 24 lata. Kasia jest dwa razy
starsza od Marysi. Uzupełnij zdania.
| 1. |
Marysia ma ______ lat, a Kasia ma _______ lat. |
| 2. |
_______ lata temu Kasia była trzy razy starsza od Marysi. |
|
 |
|
W zadaniu tym uczeń musi wykonać dokładnie te same
czynności, co w typowym rozwiązaniu zadania RO, a nie ma możliwości
prześledzenia jego toku rozumowania i zaobserwowania metody pracy z tym
zadaniem. |
|
|
|
|

typ
(WW) |
|
Kasia i Marysia mają razem 24 lata. Kasia jest dwa razy
starsza od Marysi.
A. Kasia ma 12 lat, Marysia 6.
B. Kasia ma 13 lat a Marysia 11.
C. Kasia ma 16 lat, a Marysia 8.
D. Kasia ma 18 lat, a Marysia 6. |
 |
|
Zadanie to najwygodniej rozwiązywać stosując metodę
eliminacji i preferencji. Najpierw należy odrzucić odpowiedzi niespełniające
jednego z warunków, a potem drugiego. |
|
|
|
|

typ
(WW) |
|
Kasia i Marysia mają razem 24 lata. Kasia jest dwa razy
starsza od Marysi.
Kasia była 3 razy starsza od Marysi
A. 3 lata temu
B. 8 lat temu
C. 4 lata temu
D. 10 lat temu. |
 |
|
To zadanie jest bardziej skomplikowane niż poprzednie.
Uczniowie zazwyczaj rozwiązują je otwierając to zadanie. Nie ma możliwości
prześledzenia toku rozumowania ucznia i zaobserwowania metody pracy z tym
zadaniem. Jedynie na podstawie dokonanego wyboru odpowiedzi można z dużym
prawdopodobieństwem wnioskować o popełnionych przy rozwiązywaniu zadań
błędach. |
|
|
|
|
Analizując przytoczone przykłady zadań, widać, że wybór formy
zadania w teście zależy od celu testu, od tego, co chcemy zbadać i jakie
informacje chcemy uzyskać. Aby dostać rzetelną diagnozę osiągnięć uczniów trzeba
bardzo starannie dobrać nie tylko zakres badanej wiedzy i umiejętności, ale i
formy zadań oraz sposób ich oceniania. |
|
|
|
Forma zadania |
Przydatność różnych form zadań w matematyce
ze względu na cele merytoryczne testu
|
|
L |
| n |
sprawdzanie znajomości wzorów, definicji, twierdzeń, faktów, |
| n |
uzupełnianie diagramów, wykresów, rysunków. |
|
|
KO |
| n |
sprawdzanie stosowania jednej- dwóch umiejętności
w rozwiązywaniu zadania, |
| n |
posługiwanie się językiem matematycznym. |
|
|
RO |
| n |
sprawdzanie stosowania wielu umiejętności w rozwiązywaniu
zadania, |
| n |
obserwowanie skuteczności metody przyjętej w rozwiązaniu
zadania, |
| n |
obserwowanie realizacji przyjętej metody, |
| n |
posługiwanie się językiem matematycznym. |
|
|
WW |
| n |
sprawdzanie znajomości wzorów, definicji, twierdzeń, faktów, |
| n |
uzupełnianie diagramów, wykresów, rysunków, |
| n |
sprawdzanie stosowania jednej- dwóch umiejętności
w rozwiązywaniu zadania, |
| n |
porządkowanie elementów, |
| n |
matematyzowanie sytuacji (opisywanie wyrażeniem). |
|
|
P–F |
| n |
sprawdzanie znajomości wzorów, definicji twierdzeń, faktów, |
| n |
ocenianie poprawności stwierdzeń, wyników, rysunków. |
|
|
D |
| n |
klasyfikowanie różnych elementów, |
| n |
porządkowanie elementów, |
| n |
ocena poprawności skojarzeń. |
|
|
|
|
|
|
