|
Relacje między oceną wewnątrzszkolną i zewnętrzną |
|
|
|
 |
|
Wynik ze sprawdzianu to wynik punktowy odpowiadający
poszczególnym kategoriom standardów, który trudno odnieść do ocen szkolnych
z poszczególnych przedmiotów i bloków przedmiotowych. Nasuwają się pytania:
| Jak poradzili sobie na sprawdzanie uczniowie, osiągający w szkole
podstawowej bardzo dobre wyniki z wszystkich przedmiotów? A jak Ci, którzy są bardzo dobrzy z języka polskiego albo z
matematyki? |
|
|
Podjęto próbę porównania ocen
końcoworocznych szóstoklasistów z wynikiem ze sprawdzianu 2002 na próbie 291
uczniów z pięciu szkół województwa małopolskiego. |
|
|
|
Rodzaj miejscowości,
w której mieści się szkoła |
Oznaczenie szkoły |
Liczba oddziałów
klas szóstych |
Liczba uczniów |
|
miasto powyżej 100 tysięcy mieszkańców |
A |
2 |
50 |
|
miasto powyżej 100 tysięcy mieszkańców |
B |
3 |
76 |
|
miasto powyżej 10 tysięcy mieszkańców |
C |
2 |
55 |
|
miasto poniżej 10 tysięcy mieszkańców |
D |
4 |
95 |
|
wieś |
E |
1 |
15 |
|
|
|
|
Sprawdzian adresowany był do wszystkich uczniów, ale nie
zawierał zadań z poziomu wykraczającego poza treści i umiejętności
podstawowe, typowe dla tego etapu kształcenia. Uczeń celujący nie miał
możliwości rozwiązywania zadań o podwyższonym stopniu trudności, nie miał
okazji do otrzymania takiej liczby punktów, która mogłaby go odróżnić od
ucznia bardzo dobrego. Z tego też powodu dla celów tego porównania wszystkie
oceny celujące zamieniono na oceny bardzo dobre. Nie brano pod uwagę
uczniów, których wynik punktowy na sprawdzianie był mniejszy od 5. |
|
|
|
Dzieląc wynik W ucznia na sprawdzianie 2002 (z zakresu od 5
do 40 punktów) przez 8 otrzymywano liczbę D (z zakresu od 1 do 5), którą
porównywano ze średnią S wszystkich ocen ucznia na świadectwie ukończenia
klasy VI. Po zaokrągleniu D do najbliższej liczby naturalnej otrzymywano
liczbę Z (1, 2, 3, 4 lub 5) – „stopień szkolny ze sprawdzianu”, który
porównywano z końcową oceną szóstoklasisty z języka polskiego (J) oraz
matematyki (M). Oto przykład analizy dla trzech uczniów o numerach 1, 2 i 3:
|
|
|
|
nr ucznia
|
ocena wewnątrzszkolna |
wynik sprawdzianu (W)
|
Wynik sprawdzianu podzielony przez 8
|
|
średnia (S) |
polski (J)
|
matematyka (M)
|
|
dokładny (D)
|
w zaokrągleniu (Z)
|
|
1 |
4,35 |
4 |
5 |
37 |
4,625 |
5 |
|
2 |
4,2 |
3 |
5 |
33 |
4,125 |
4 |
|
3 |
3,95 |
4 |
4 |
30 |
3,75 |
4 |
|
|
|
|
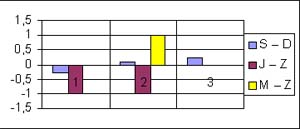
nr ucznia |
S – D |
J – Z |
M – Z |
|
1 |
-0,275 |
-1 |
0 |
|
2 |
0,075 |
-1 |
1 |
|
3 |
0,2 |
0 |
0 |
|
|
 |
|
|
|
|
Na podstawie przedstawionych informacji widać, że we
wszystkich trzech przypadkach średnia S ocen szkolnych dobrze korelowała z
liczbą D. Stopień J z języka polskiego w dwóch przypadkach był niższy o 1 od
Z – „stopnia ze sprawdzianu”, a w jednym przypadku był taki sam. Pełna
zgodność stopni M i Z wystąpiła w dwóch przypadkach, uczeń nr 2 otrzymał z
matematyki stopień M wyższy o 1 niż stopień Z. Informacje te zilustrowano na
diagramie.
Dla 70 procent z 291 szóstoklasistów różnica między
średnią wszystkich ich ocen na świadectwie i liczbą D (wynikiem W
sprawdzianu podzielonym przez 8) była mniejsza od 0,5. Także dla 70 procent
tych uczniów średnia S była wyższa od liczby D. Wynik oceny wewnątrzszkolnej
przewyższał wynik oceny zewnętrznej. |
|
|
|
Różnica stopni z języka polskiego J i ze sprawdzianu Z
|
Różnica stopni z matematyki M i ze sprawdzianu Z |
|
J – Z |
Liczba uczniów |
% uczniów |
|
-2 |
11 |
3,8 |
29,2 |
|
-1 |
74 |
25,4 |
|
0 |
150 |
52 |
52 |
|
1 |
51 |
17,5 |
19,2 |
|
2 |
5 |
1,7 |
|
|
M – Z |
Liczba uczniów |
% uczniów |
|
-3 |
2 |
0,7 |
28,5 |
|
-2 |
11 |
3,8 |
|
-1 |
70 |
24 |
|
0 |
169 |
58 |
58 |
|
1 |
36 |
12,4 |
13,4 |
|
2 |
3 |
1 |
|
|
|
|
|
Więcej niż 50 procent uczniów otrzymało stopień Z ze
sprawdzianu zgodny z końcowym stopniem J z języka
polskiego. U blisko 60% uczniów taka zgodność wystąpiła między stopniami M z
matematyki i Z – ze sprawdzianu. Dla 95% uczniów stopień Z ze sprawdzianu
różnił się nie więcej niż o 1 od stopnia J z języka polskiego. Taka sama
prawidłowość wystąpiła w przypadku matematyki. Blisko 30% uczniów otrzymało
na sprawdzianie stopień niższy niż z języka polskiego (podobnie w przypadku
matematyki).
|
|
|
|
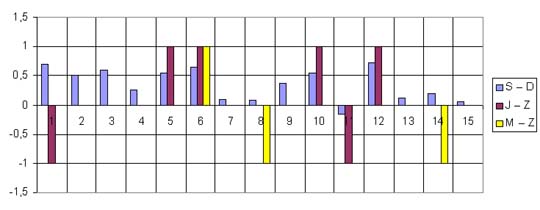
Diagramy różnic między oceną wewnątrzszkolną i
zewnętrzną dla poszczególnych szkół |
|
|
| SZKOŁA A |
 |
oddział A |
|
|
 |
| SZKOŁA A |
 |
oddział B |
|
|
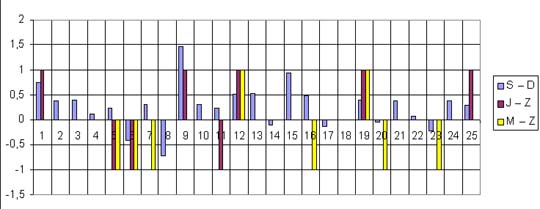 |
| SZKOŁA B |
 |
oddział A |
|
|
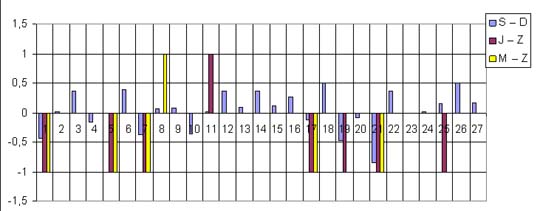 |
| SZKOŁA B |
 |
oddział B |
|
|
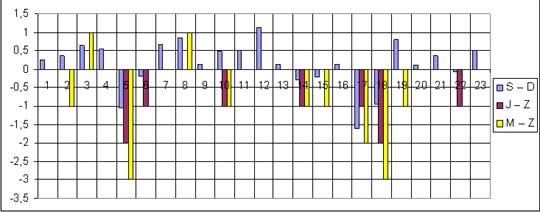 |
| SZKOŁA B |
 |
oddział C |
|
|
 |
| SZKOŁA C |
 |
oddział A |
|
|
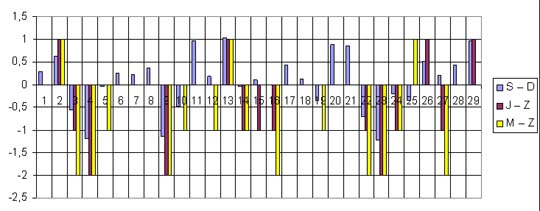 |
| SZKOŁA C |
 |
oddział B |
|
|
 |
| SZKOŁA D |
 |
oddział A |
|
|
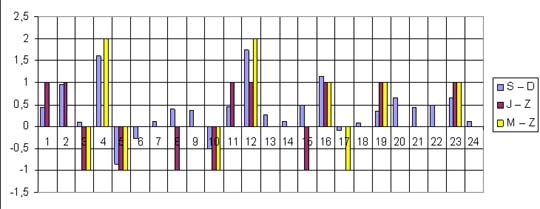 |
| SZKOŁA D |
 |
oddział B |
|
|
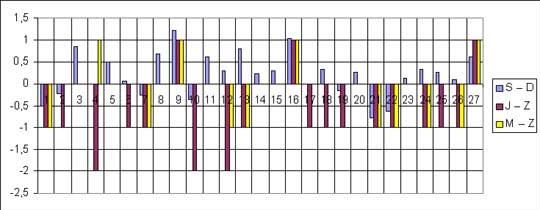 |
| SZKOŁA D |
 |
oddział C |
|
|
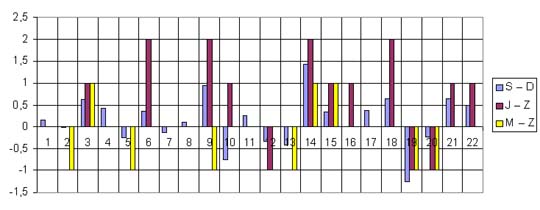 |
| SZKOŁA D |
 |
oddział D |
|
|
 |
| SZKOŁA E |
 |
oddział A |
|
|
 |
|
|
|
Warto przeanalizować wyniki poszczególnych szkół
czy oddziałów klasowych. Np.: |
| u |
W szkole B w oddziale B u wszystkich uczniów oceny Z ze
sprawdzianu były nie niższe od ocen J z języka
polskiego. |
| u |
W szkole E tylko jeden uczeń ma niższą średnią S niż
liczba D. |
| u |
W szkole E zgodność oceny M z matematyki z oceną Z ze
sprawdzianu odnotowano u większości szóstoklasistów. |
| u |
W szkole B u większości uczniów oceny Z ze sprawdzianu
były wyższe lub takie same jak oceny J z języka
polskiego i M z matematyki. |
| u |
W szkole A u większości uczniów oceny Z ze sprawdzianu
były niższe lub takie same jak oceny J z języka
polskiego i M z matematyki. |
|
|
Wynik ze sprawdzianu nie powinien być
zaskoczeniem dla ucznia, a jedynie potwierdzeniem jego osiągnięć.
|
